Generalized Linear Models
Both linear models and ANOVA have the standard assumptions of independent and identically distributed normal random variables.
Certain kinds of response variables generally contravene these assumptions, and generalized linear models (GLMs) are excellent at dealing with them.
The use of GLMs is recommended either when:
- the variance is not constant, and/or
- the errors are not normally distributed.
Specifically, you should use GLMs when the response variable is:
- count data expressed as proportions (e.g. logistic regressions);
- count data that are not proportions (e.g. log-linear models of counts);
- binary response variables (e.g. dead or alive);
- data on time to death where the variance increases faster than linearly with the mean (e.g. time data with gamma errors).
The central assumption that we have made up to this point is that variance was constant. In count data, however, where the response variable is an integer and there are often lots of zeros in the dataframe, the variance may increase linearly with the mean. With proportion data, where we have a count of the number of failures of an event as well as the number of successes, the variance will be an inverted U-shaped function of the mean. Where the response variable follows a gamma distribution (as in time-to-death data) the variance increases faster than linearly with the mean. Many of the basic statistical methods such as regression and Student's t test assume that variance is constant, but in many applications this assumption is untenable. Hence the great utility of GLMs.
A generalized linear model has three important properties:
- the error structure;
- the linear predictor;
- the link function.
Up to this point, we have dealt with the statistical analysis of data with normal errors. In practice, however, many kinds of data have non-normal errors, for example:
- errors that are strongly skewed;
- errors that are kurtotic;
- errors that are strictly bounded (as in proportions);
- errors that cannot lead to negative fitted values (as in counts).
In the past, the only tools available to deal with these problems were transformation of the response variable or the adoption of non-parametric methods. A GLM allows the specification of a variety of different error distributions:
- Poisson errors, useful with count data;
- binomial errors, useful with data on proportions;
- gamma errors, useful with data showing a constant coefficient of variation;
- exponential errors, useful with data on time to death (survival analysis).
The error structure is defined by means of the family argument, used as part of the model formula. Examples are glm(y ~ z, family = poisson) which means that the response variable y has Poisson errors, and glm(y ~ z, family = binomial) which means that the response is binary, and the model has binomial errors.
As with previous models, the explanatory variable z can be continuous (leading to a regression analysis) or categorical (leading to an ANOVA-like procedure called analysis of deviance)
Types of GLM
Count data (Poisson)
Input and display count data
clusters <- read.table("../data/clusters.txt", header = TRUE)
head(clusters)## Cancers Distance
## 1 0 11.47
## 2 0 66.55
## 3 0 47.46
## 4 0 48.38
## 5 0 73.77
## 6 0 70.58hist(clusters$Cancers)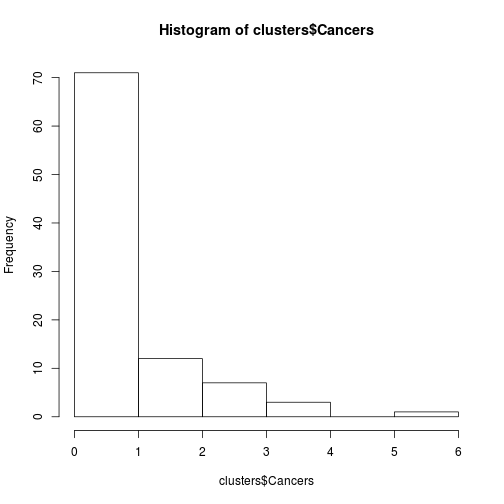
Fig. Histogram of some count data
plot(clusters$Distance, clusters$Cancers)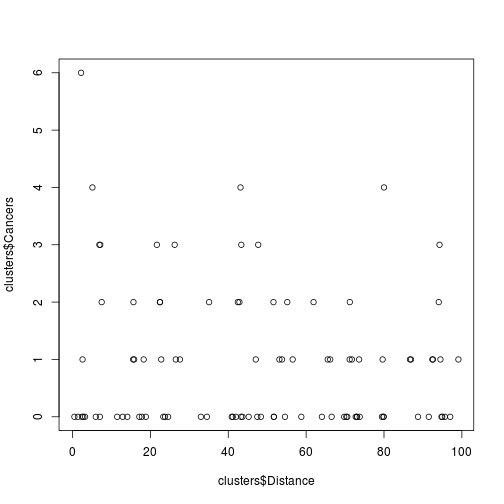
Fig. Plot of cancers on distance
Run a GLM using a Poisson error distribution
model1 <- glm(formula = Cancers ~ Distance, family = poisson, data = clusters)
summary(model1)##
## Call:
## glm(formula = Cancers ~ Distance, family = poisson, data = clusters)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.550 -1.349 -1.155 0.388 3.130
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.18686 0.18873 0.99 0.322
## Distance -0.00614 0.00367 -1.67 0.094 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 149.48 on 93 degrees of freedom
## Residual deviance: 146.64 on 92 degrees of freedom
## AIC: 262.4
##
## Number of Fisher Scoring iterations: 5check for overdispersion
model2 <- glm(Cancers ~ Distance, family = quasipoisson, data = clusters)
summary(model2)##
## Call:
## glm(formula = Cancers ~ Distance, family = quasipoisson, data = clusters)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.550 -1.349 -1.155 0.388 3.130
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.18686 0.23536 0.79 0.43
## Distance -0.00614 0.00457 -1.34 0.18
##
## (Dispersion parameter for quasipoisson family taken to be 1.555)
##
## Null deviance: 149.48 on 93 degrees of freedom
## Residual deviance: 146.64 on 92 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 5Binomial: binary response
Binomial data can either be modelled at the individual (binary response) or group (proportion) level.
At the individual level we can model each individual in terms of dead or alive (male/female, tall/short, green/red, ...).
Read in some binomial data looking at the incidence (presence = 1, absence = 0) of a thing in a variety of places of different sizes (area) and distances (isolation) from a giant place.
isol <- read.table("../data/isolation.txt", header = TRUE)
head(isol)## incidence area isolation
## 1 1 7.928 3.317
## 2 0 1.925 7.554
## 3 1 2.045 5.883
## 4 0 4.781 5.932
## 5 0 1.536 5.308
## 6 1 7.369 4.934We begin by fitting a complex model involving an interaction between isolation and area:
model1 <- glm(incidence ~ area * isolation, family = binomial, data = isol)Then we fit a simpler model with only main effects for isolation and area:
model2 <- glm(incidence ~ area + isolation, family = binomial, data = isol)We now can compare the two models as before using ANOVA. In the case of binary data, we need to do a Chi-squared test.
anova(model1, model2, test = "Chi")## Analysis of Deviance Table
##
## Model 1: incidence ~ area * isolation
## Model 2: incidence ~ area + isolation
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 46 28.2
## 2 47 28.4 -1 -0.15 0.7summary(model2)##
## Call:
## glm(formula = incidence ~ area + isolation, family = binomial,
## data = isol)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.819 -0.309 0.049 0.363 2.119
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 6.642 2.922 2.27 0.023 *
## area 0.581 0.248 2.34 0.019 *
## isolation -1.372 0.477 -2.88 0.004 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 68.029 on 49 degrees of freedom
## Residual deviance: 28.402 on 47 degrees of freedom
## AIC: 34.4
##
## Number of Fisher Scoring iterations: 6Plotting binary response data
To plot the fitted line of a generalized linear model, we generally have to use the predict() function, because the model, although linear, is not a straight line that can be plotted with either an intercept or slope, as we used for lm() and abline(). In this case, we also need to set type = "response".
# run two models, one for area and one for isolation
modela <- glm(incidence ~ area, family = binomial, data = isol)
modeli <- glm(incidence ~ isolation, family = binomial, data = isol)
# set up a two-panel plotting area
par(mfrow = c(1, 2))
# use the predict() function to create the fitted y values
## 1. area
# create a sequence of x values
xv <- seq(0, 9, 0.01)
# y values
yv <- predict(modela, list(area = xv), type = "response")
# plot the raw data
plot(isol$area, isol$incidence)
# use the lines function to add the fitted lines
lines(xv, yv)
## 2. isolation
xv2 <- seq(0, 10, 0.1)
yv2 <- predict(modeli, list(isolation = xv2), type = "response")
plot(isol$isolation, isol$incidence)
lines(xv2, yv2)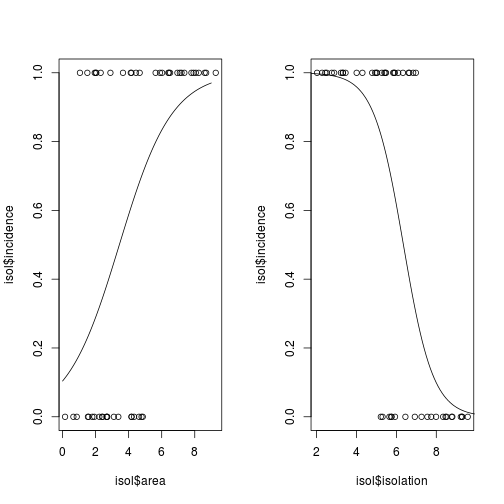
Fig. Plotting binary response variables
Binomial: Proportion data
At the group level, we look at the proportion of successes and failures (or male/famale, tall/short, ...) in groups/populations/sites.
In this case, we have the number of males and females in a range of populations. Does sex ratio vary with population size?
numbers <- read.table("../data/sexratio.txt", header = TRUE)
head(numbers)## density females males
## 1 1 1 0
## 2 4 3 1
## 3 10 7 3
## 4 22 18 4
## 5 55 22 33
## 6 121 41 80We will begin by plotting the proportion of males, both as normal and on a log scale.
par(mfrow = c(1, 2))
p <- numbers$males/(numbers$males + numbers$females)
plot(numbers$density, p, ylab = "Proportion male")
plot(log(numbers$density), p, ylab = "Proportion male")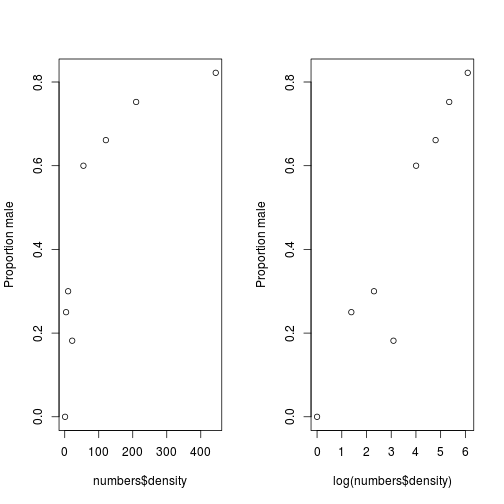
Fig. Plotting proportion data
To model proportion data, R requires a unique form of the response variable - a matrix of two columns of successes and failures, in this case males and females.
y <- cbind(numbers$males, numbers$females)
y## [,1] [,2]
## [1,] 0 1
## [2,] 1 3
## [3,] 3 7
## [4,] 4 18
## [5,] 33 22
## [6,] 80 41
## [7,] 158 52
## [8,] 365 79model <- glm(y ~ numbers$density, family = binomial)
summary(model)##
## Call:
## glm(formula = y ~ numbers$density, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.462 -1.276 -0.991 0.574 1.880
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.080737 0.155038 0.52 0.6
## numbers$density 0.003510 0.000512 6.86 6.8e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 71.159 on 7 degrees of freedom
## Residual deviance: 22.091 on 6 degrees of freedom
## AIC: 54.62
##
## Number of Fisher Scoring iterations: 4
model <- glm(y ~ log(numbers$density), family = binomial)
summary(model)##
## Call:
## glm(formula = y ~ log(numbers$density), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.970 -0.341 0.150 0.402 1.037
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.6593 0.4876 -5.45 4.9e-08 ***
## log(numbers$density) 0.6941 0.0906 7.66 1.8e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 71.1593 on 7 degrees of freedom
## Residual deviance: 5.6739 on 6 degrees of freedom
## AIC: 38.2
##
## Number of Fisher Scoring iterations: 4