Mixed effects models
Generalized Linear Mixed Effects Model: Example Using Seedling Survival Data
What is the response variable?
exploring the data
# read in data file
sdata <- read.table("../data/seedling-survival-data.txt", header = TRUE, as.is = TRUE,
sep = "\t")
head(sdata)## PLOT SPECIES HEIGHT STATUS LIGHT CONS CONBA
## 1 1 PSYBRA 52 1 0.205 1 18.0165
## 2 1 PIPGLA 40 1 0.205 1 0.8992
## 3 1 PIPGLA 33 0 0.205 1 0.8992
## 4 1 ANDINE 41 0 0.205 0 0.0000
## 5 1 PREMON 90 1 0.205 6 3633.1027
## 6 1 SLOBER 130 1 0.205 1 67.5457Let's explore the data a bit more.
How many lived & died?
table(sdata$STATUS)##
## 0 1
## 2718 1967Look at ranges and distributions of your predictor variables
par(mfrow = c(1, 3))
range(sdata$CONS)## [1] 0 243hist(sdata$CONS, breaks = 50)
range(sdata$LIGHT)## [1] 0.069 0.946hist(sdata$LIGHT, breaks = 10)
range(sdata$HEIGHT)## [1] 10 600hist(sdata$HEIGHT, breaks = 50)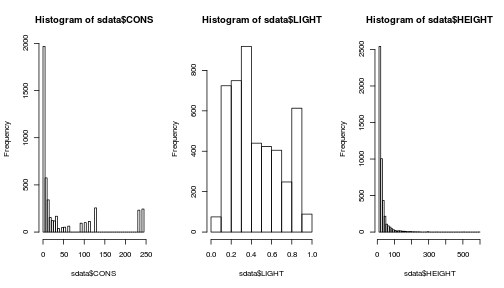
Fig. Histograms of predictor variables
Note that your predictors have very different ranges so, if you want to directly compare the effects or test for interactions, you should rescale them by subtracting the mean and dividing by the standard deviation.
sdata$LIGHT.ADJ <- (sdata$LIGHT - mean(sdata$LIGHT))/sd(sdata$LIGHT)
sdata$HEIGHT.ADJ <- (sdata$HEIGHT - mean(sdata$HEIGHT))/sd(sdata$HEIGHT)
sdata$CONS.ADJ <- (sdata$CONS - mean(sdata$CONS))/sd(sdata$CONS)start analyzing
Load library to do mixed effects models
library(lme4)## Loading required package: lattice
## Loading required package: Matrix
## Loading required package: methodsFirst, run a simple model with only height as a predictor
surv.glm <- glm(sdata$STATUS ~ sdata$HEIGHT.ADJ, family = binomial)
surv.glmer <- glmer(formula = STATUS ~ HEIGHT.ADJ + (1 | PLOT), data = sdata,
family = binomial)
summary(surv.glm)##
## Call:
## glm(formula = sdata$STATUS ~ sdata$HEIGHT.ADJ, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.072 -0.979 -0.922 1.316 1.465
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.3049 0.0306 -9.97 <2e-16 ***
## sdata$HEIGHT.ADJ 0.5943 0.0455 13.05 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 6373.9 on 4684 degrees of freedom
## Residual deviance: 6129.9 on 4683 degrees of freedom
## AIC: 6134
##
## Number of Fisher Scoring iterations: 4summary(surv.glmer)## Generalized linear mixed model fit by maximum likelihood ['glmerMod']
## Family: binomial ( logit )
## Formula: STATUS ~ HEIGHT.ADJ + (1 | PLOT)
## Data: sdata
##
## AIC BIC logLik deviance
## 5649 5669 -2822 5643
##
## Random effects:
## Groups Name Variance Std.Dev.
## PLOT (Intercept) 0.669 0.818
## Number of obs: 4685, groups: PLOT, 148
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.2335 0.0798 -2.92 0.0034 **
## HEIGHT.ADJ 0.6490 0.0532 12.21 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## HEIGHT.ADJ 0.028Is it necessary to include PLOT as a random effect?
Test this using likelihood ratio test, as recommended by Bolker et al. 2009
LL1 <- logLik(surv.glm)
LL2 <- logLik(surv.glmer)
D <- as.numeric(-2 * (LL1 - LL2))
pchisq(D, df = 1, lower = FALSE)[1]## [1] 7.462e-108Now compare adding species as a fixed vs. a random effect
surv.glm.spp <- glm(STATUS ~ SPECIES + HEIGHT.ADJ, data = sdata, family = binomial)
surv.glmer.spp <- glmer(STATUS ~ HEIGHT.ADJ + (1 | PLOT) + (1 | SPECIES), data = sdata,
family = binomial)
summary(surv.glm.spp)##
## Call:
## glm(formula = STATUS ~ SPECIES + HEIGHT.ADJ, family = binomial,
## data = sdata)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.673 -0.859 -0.667 0.956 2.576
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.8855 0.6934 -1.28 0.20155
## SPECIESALCLAT -1.4111 0.7701 -1.83 0.06691 .
## SPECIESANDINE 1.1706 0.8178 1.43 0.15228
## SPECIESARDGLA 16.8536 1455.3977 0.01 0.99076
## SPECIESARDOBO -14.3010 1455.3977 -0.01 0.99216
## SPECIESBUCTET 16.6510 1455.3977 0.01 0.99087
## SPECIESBYRSPI 1.0029 0.7258 1.38 0.16701
## SPECIESCALCAL 1.6398 1.1017 1.49 0.13663
## SPECIESCASARB 2.3372 0.7996 2.92 0.00347 **
## SPECIESCASSYL 3.2977 1.2590 2.62 0.00881 **
## SPECIESCECSCH -3.7088 1.3946 -2.66 0.00783 **
## SPECIESCHIDOM 0.8793 0.8959 0.98 0.32634
## SPECIESCLIERO -15.0637 998.0202 -0.02 0.98796
## SPECIESCLUROS -14.2785 1455.3977 -0.01 0.99217
## SPECIESCOMGLA 15.3951 1013.9037 0.02 0.98789
## SPECIESCORBOR 3.2011 1.2659 2.53 0.01145 *
## SPECIESCORSUL -14.8672 828.8543 -0.02 0.98569
## SPECIESCROPOE 3.0876 1.0291 3.00 0.00270 **
## SPECIESCSSGUI -14.4136 1455.3977 -0.01 0.99210
## SPECIESDACEXC -1.7054 0.9144 -1.86 0.06218 .
## SPECIESDENARB -0.4376 1.4256 -0.31 0.75885
## SPECIESDRYGLA -14.5262 1455.3977 -0.01 0.99204
## SPECIESEUGDOM 1.7217 0.8083 2.13 0.03316 *
## SPECIESEUGSTA 3.0465 1.2682 2.40 0.01630 *
## SPECIESFAROCC 2.0613 1.3308 1.55 0.12141
## SPECIESGONSPI 16.1289 473.8314 0.03 0.97285
## SPECIESGUAGLA 1.4396 0.9494 1.52 0.12942
## SPECIESGUAGUI 0.1033 0.6966 0.15 0.88215
## SPECIESGUEVAL -14.4361 1455.3977 -0.01 0.99209
## SPECIESGUTCAR 0.0589 1.3502 0.04 0.96518
## SPECIESHIRRUG 1.1565 0.8638 1.34 0.18061
## SPECIESHOMRAC 1.7935 0.8171 2.19 0.02817 *
## SPECIESINGLAU 1.7515 0.7028 2.49 0.01269 *
## SPECIESINGVER 1.4364 0.8462 1.70 0.08962 .
## SPECIESIXOFER 1.7528 0.7607 2.30 0.02121 *
## SPECIESLAEPRO -0.9416 1.2929 -0.73 0.46644
## SPECIESLASLAN 16.5868 726.9454 0.02 0.98180
## SPECIESMANBID 1.9517 0.7387 2.64 0.00824 **
## SPECIESMARNOB 1.8252 1.4090 1.30 0.19519
## SPECIESMATDOM -0.4728 0.8058 -0.59 0.55732
## SPECIESMELHER -14.7064 1455.3977 -0.01 0.99194
## SPECIESMICIMP 12.4625 1455.3977 0.01 0.99317
## SPECIESMICPRA 15.5709 530.9309 0.03 0.97660
## SPECIESMICRAC 16.2498 830.2057 0.02 0.98438
## SPECIESMYRDEF 1.0401 1.2113 0.86 0.39050
## SPECIESMYRLEP 3.1196 1.2627 2.47 0.01349 *
## SPECIESMYRSPL 2.1950 0.8976 2.45 0.01447 *
## SPECIESOCOLEU 2.9209 0.7717 3.78 0.00015 ***
## SPECIESOCOSIN 1.6466 0.7281 2.26 0.02372 *
## SPECIESORMKRU -14.4316 1455.3977 -0.01 0.99209
## SPECIESPALRIP -1.2481 0.7914 -1.58 0.11476
## SPECIESPHYICO -14.4136 1455.3977 -0.01 0.99210
## SPECIESPIPBLA 16.5834 1455.3977 0.01 0.99091
## SPECIESPIPGLA 0.3960 0.7138 0.55 0.57908
## SPECIESPIPHIS 1.9153 1.3606 1.41 0.15921
## SPECIESPREMON 0.3689 0.6972 0.53 0.59674
## SPECIESPSESPU 2.6686 1.2905 2.07 0.03865 *
## SPECIESPSYBER -0.1923 0.7078 -0.27 0.78583
## SPECIESPSYBRA 0.4080 0.7284 0.56 0.57543
## SPECIESPSYDEF 2.0402 0.9691 2.11 0.03527 *
## SPECIESPSYMAL 1.6238 0.8066 2.01 0.04411 *
## SPECIESRHEPOR 12.2664 1006.7881 0.01 0.99028
## SPECIESROYBOR -2.4099 1.0013 -2.41 0.01610 *
## SPECIESSAPLAU -0.1434 0.7259 -0.20 0.84341
## SPECIESSCHMOR 0.4305 0.7239 0.59 0.55200
## SPECIESSLOBER 1.6228 0.7577 2.14 0.03221 *
## SPECIESSYMMAR 16.6284 1455.3977 0.01 0.99088
## SPECIESSYZJAM 1.9873 0.7743 2.57 0.01027 *
## SPECIESTABHET 1.0586 0.7139 1.48 0.13811
## SPECIESTETBAL 1.7468 0.7963 2.19 0.02826 *
## SPECIESTRIPAL 0.8344 0.7299 1.14 0.25297
## SPECIESZANMAR 0.3912 0.8390 0.47 0.64098
## HEIGHT.ADJ 0.7234 0.0594 12.18 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 6373.9 on 4684 degrees of freedom
## Residual deviance: 5316.4 on 4612 degrees of freedom
## AIC: 5462
##
## Number of Fisher Scoring iterations: 14summary(surv.glmer.spp)## Generalized linear mixed model fit by maximum likelihood ['glmerMod']
## Family: binomial ( logit )
## Formula: STATUS ~ HEIGHT.ADJ + (1 | PLOT) + (1 | SPECIES)
## Data: sdata
##
## AIC BIC logLik deviance
## 5242 5268 -2617 5234
##
## Random effects:
## Groups Name Variance Std.Dev.
## PLOT (Intercept) 0.67 0.819
## SPECIES (Intercept) 2.06 1.434
## Number of obs: 4685, groups: PLOT, 148; SPECIES, 72
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.0855 0.2150 0.4 0.69
## HEIGHT.ADJ 0.8298 0.0651 12.8 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## HEIGHT.ADJ 0.010Linear Mixed Effects Model: Example Using Fruit Production Data With Repeated Measures
In this case we have normally-distributed errors.
exploring the data
The lmer() function does not return p values because of uncertainties in calculating the appropriate degrees of freedom, but there are some work arounds.
# read in data
fruitdata <- read.table("../data/fruit-data.txt", header = TRUE, as.is = TRUE,
sep = "\t")
head(fruitdata)## TAG DBH FRUIT YEAR
## 1 86 454 45 1
## 2 86 454 662 2
## 3 101 369 6 1
## 4 101 369 7 2
## 5 155 450 700 1
## 6 155 450 225 2The fruit production is log normally distributed, so we can make it normally distributed by log transforming it. Why do we add +1 to each value in this case?
fruitdata$LOGFRUIT <- log(fruitdata$FRUIT + 1)
par(mfrow = c(1, 2))
hist(fruitdata$FRUIT)
hist(fruitdata$LOGFRUIT)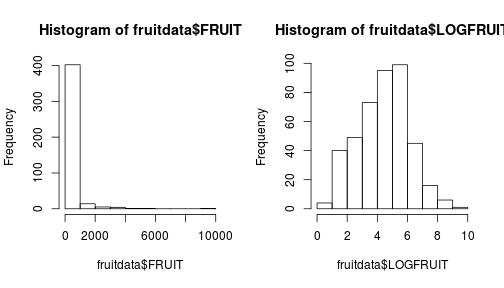
Fig. Histograms of fruit production
Let's plot the relationship we are trying to model
plot(fruitdata$DBH, fruitdata$LOGFRUIT)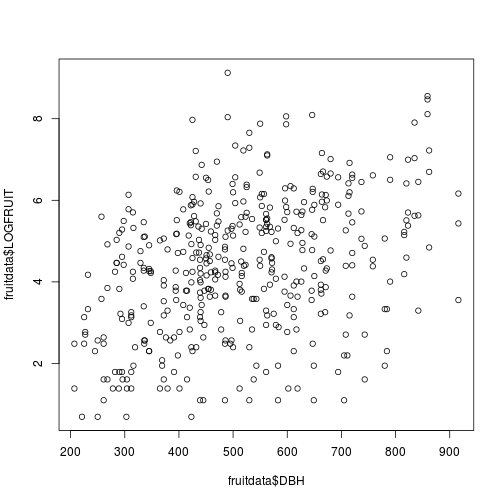
Fig. Fruit production as a function of tree size
We have 3 years of fruit production data, with the same individuals measured in each year (ie. repeated measures) which we can account for by including individual as a random effect
fruit.lmer <- lmer(LOGFRUIT ~ as.factor(YEAR) + DBH + (1 | TAG), data = fruitdata)
summary(fruit.lmer)## Linear mixed model fit by REML ['lmerMod']
## Formula: LOGFRUIT ~ as.factor(YEAR) + DBH + (1 | TAG)
## Data: fruitdata
##
## REML criterion at convergence: 1532
##
## Random effects:
## Groups Name Variance Std.Dev.
## TAG (Intercept) 0.825 0.908
## Residual 1.416 1.190
## Number of obs: 428, groups: TAG, 179
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 2.267673 0.311076 7.29
## as.factor(YEAR)2 0.532925 0.143737 3.71
## as.factor(YEAR)3 -0.528386 0.142406 -3.71
## DBH 0.003991 0.000572 6.98
##
## Correlation of Fixed Effects:
## (Intr) a.(YEAR)2 a.(YEAR)3
## as.f(YEAR)2 -0.180
## as.f(YEAR)3 -0.214 0.446
## DBH -0.927 -0.020 0.009As with other models we have seen, for factors the estimates are relative to the Intercept, which is the value for the first factor (in this case, YEAR 1)
In this case, we do not test whether we should include individual (TAG) in the model because we know we need to control for repeated measures, so we should keep it in.
R 3.0.0 and above
For the latest recommendations see here.
< R 3.0.0
Since lmer() does not give p values, in older versions of R we can evaluate significance using confidence intervals based on simulations, using two functions: mcmcsamp() and HPDinterval().
The function mcmcsamp() generates a sample of size n from the posterior distribution of the parameters of our fitted model using Markov Chain Monte Carlo methods ...
fruit.mcmc <- mcmcsamp(fruit.lmer, n = 1000) # in reality, may want to use a larger n (eg. 10,000).... to then generate 95% "confidence" intervals, we use HPDinterval with prob = 0.95 for each parameter, it returns the shortest interval with a 95% probability content in the empirical distribution.
HPDinterval() is included in two packages (code & lme4), and only the lme4 version seems to be working, so we have to specific lme4
lme4::HPDinterval(fruit.mcmc, prob = 0.95) Best yet, there is this function, in the languageR package, which does all of this for you in one step:
library('languageR')
pvals.fnc(fruit.lmer, nsim = 1000) For the latest recommendations see here.
And for previous discussions and far more details than you really want on this issue, see here and related posts.
Exercises
Using the seedling survival data, try adding other fixed effects (eg. light, conspecific neighbors) to the model.
How do your results change when you add/remove PLOT as a random effect?